Como ya venimos viendo los lugares geométricos de las cónicas en esta ocasión veremos la hipérbola.Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
Las componentes de esta son:
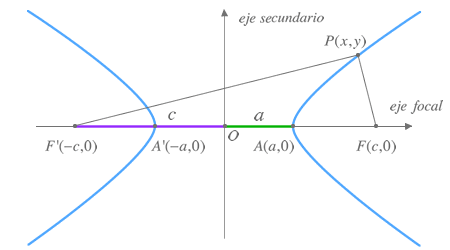
Focos: Son los puntos fijos F y F'.
Eje principal o real: Es la recta que pasa por los focos.
Eje secundario o imaginario: Es la mediatriz del segmento FF'.
Centro: Es el punto de intersección de los ejes.
Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal. Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
Distancia focal: Es el segmento de longitud 2c.
Eje mayor: Es el segmento de longitud 2a.
Eje menor: Es el segmento de longitud 2b.
Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
Asíntotas: Son las rectas de ecuaciones:

Relación entre los semiejes:

Ecuación de la hipérbola:

No hay comentarios:
Publicar un comentario